ZONeエナジーのプログラミングイベント “HELLO SPACE” の3問目の記事です。
3問目は与えられたグラフ（ノードとエッジのリスト）について処理する問題で、これをRustで解きました。

ちなみに過去記事はこちら：
1問目（rot13）
2問目（素数判定）

お題３

例題

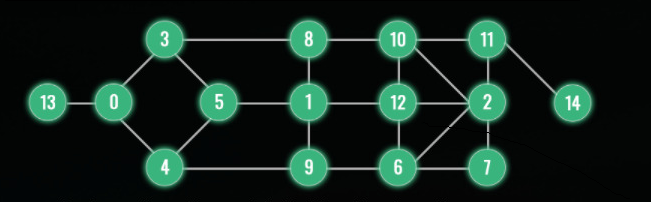
以下の

のようなグラフが与えられるとき、3つのノードを選択してなるべく多くの隣接ノードとなるようにする、という問題。例えば

0, 1, 2

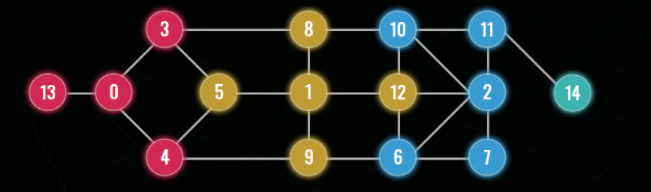
のノードを選択すると、それぞれに隣接しているノードは

のように赤●、黄色●、青●で表され、ノード14以外はすべて隣接している。この組み合わせが最も多くのノードが隣接する組み合わせである。

と言うように、3つのノードを選択してなるべく多くのノードが隣接しているようにするという問題です。

本題

本当に解くべきデータでは、ノード50個、エッジ500個のデータになります：

question3.txt

かっこいい解き方は思いつかなかったので、真正面から考えました。つまり、50個のノードから3個選ぶ組み合わせのそれぞれについて隣接ノードをカウントし、そのカウントが最大化される組み合わせを選ぶようします。組み合わせ数は 50C3 = 19600 通り。この中から隣接ノード数が最大のものを選びます。

コードは以下の通り：

question3.rs

use std::io;
use std::io::prelude::*;
use std::collections::btree_set::BTreeSet;
use std::collections::hash_map::HashMap;

#[derive(Debug)]
struct Edge {
    node0: usize,
    node1: usize
}

#[derive(Debug, Clone)]
struct Node {
    neighbors: Vec<usize>
}

fn main() {

    let (nodes, edges) = load(&mut io::BufReader::new(io::stdin()));

    println!("edges.len()={}", edges.len());

    println!("edges={:?}", edges);

    println!("nodes={:?}", nodes);

    // どれだけNodeを塗りつぶせるか

    let mut map = HashMap::new();

    // 3つを選ぶ組み合わせ
    let end = nodes.len();

    //[元の実装]ここから
    // for i in 0..(end - 2) {
    //     for j in (i + 1)..(end - 1){
    //         for k in (j + 1)..end {
    //             let rel_nodes_set = get_releted_nodes_set(&nodes, i, j, k);
    //             map.insert((i, j, k), rel_nodes_set.len());
    //         }
    //     }
    // }
    //[元の実装]ここまで

    //[Iteratorを使ったおまけ実装]ここから
    for triple in tri_combi(end) {
        let (i, j, k) = triple;
        let rel_nodes_set = get_releted_nodes_set(&nodes, i, j, k);
        map.insert((i, j, k), rel_nodes_set.len());
    }
    //[Iteratorを使ったおまけ実装]ここまで

    println!("{:?}", map);

    let max_elem = map.iter().max_by(|x, y| x.1.cmp(y.1)).unwrap();
    println!("{:?}", max_elem);
}

// ある組み合わせについて
// 関連する星(Node)のインデックス集合を取得する
fn get_releted_nodes_set(nodes: &Vec<Node>, node_i: usize, node_j: usize, node_k: usize) -> BTreeSet<usize> {
    let mut set: BTreeSet<usize> = BTreeSet::new();
    set.insert(node_i);
    for i in &nodes[node_i].neighbors {
        set.insert(*i);
    }
    set.insert(node_j);
    for j in &nodes[node_j].neighbors {
        set.insert(*j);
    }
    set.insert(node_k);
    for k in &nodes[node_k].neighbors {
        set.insert(*k);
    }
    set
}

fn load(reader: &mut dyn BufRead) -> (Vec<Node>, Vec<Edge>) {
    let mut input = String::new();
    let mut nodes: Vec<Node> = Vec::new();
    let mut edges: Vec<Edge> = Vec::new();

    // 一行目読込
    reader.read_line(&mut input).unwrap();
    let firstline_values: Vec<usize> = input
        .trim()
        .split_whitespace()
        .map(|w| w.parse::<usize>().unwrap())
        .collect();
    input.clear();

    // Nodeを必要な数作成
    nodes.resize(firstline_values[0] as usize, Node{ neighbors: Vec::<usize>::new() });

    while reader.read_line(&mut input).unwrap() > 0 {
        let line_values: Vec<usize> = input
            .trim()
            .split_whitespace()
            .map(|w| w.parse::<usize>().unwrap())
            .collect();
        input.clear();
        
        // Edge作成
        let edge = Edge {
            node0: line_values[0],
            node1: line_values[1]
        };
        edges.push(edge);

        // Nodeにリンクを設定
        nodes[line_values[0] as usize].neighbors.push(line_values[1]);
        nodes[line_values[1] as usize].neighbors.push(line_values[0]);
    }

    (nodes, edges)
}

// ここから下はおまけ。Iteratorを使った実装の実験です。

struct TriCombi {
    triple: (usize, usize, usize),
    max_exclusive: usize
}

impl Iterator for TriCombi {
    type Item = (usize, usize, usize);

    fn next(&mut self) -> Option<Self::Item> {
        let result_triple = self.triple;
        let (mut i, mut j, mut k) = self.triple;
        if i == self.max_exclusive - 2 {
            return None;
        }

        k += 1;
        if k == self.max_exclusive {
            j += 1;
            if j == self.max_exclusive - 1 {
                i += 1;
                j = i + 1;
            }
            k = j + 1;
        }
        self.triple = (i, j, k);
        
        Some(result_triple)
    }
}

fn tri_combi(max_exclusive: usize) -> TriCombi{
    TriCombi { triple: (0, 1, 2),  max_exclusive: max_exclusive}
}

このコードで正解が出せました。

使用例

(入力ファイル名をquestion3.txtとする)

> question3.exe < question3.txt

解説

メモリをあまり使わないようにするのであれば、組み合わせをたどる際にそれまで最大であったデータだけ持っていればいいでしょうが、せっかくなのでRustのHashMapを使っています。

load()関数で入力ファイルを解析していますが、結果のノードリスト、エッジのリストをタプルに入れていっぺんに返せるのがいいですね：

fn load(reader: &mut dyn BufRead) -> (Vec<Node>, Vec<Edge>)

私がメインに使っているJavaではタプルが無いので、複数のオブジェクトを返したいときに工夫が要りますが、Rustにはタプルがあって便利です。

それから、これも余計な実装ですが、main()関数中：

    //[元の実装]ここから
    // for i in 0..(end - 2) {
    //     for j in (i + 1)..(end - 1){
    //         for k in (j + 1)..end {
    //             let rel_nodes_set = get_releted_nodes_set(&nodes, i, j, k);
    //             map.insert((i, j, k), rel_nodes_set.len());
    //         }
    //     }
    // }
    //[元の実装]ここまで

が、元々の実装でこれで問題なく動作します。が、Iteratorをやってみたかったので現在の実装になっています。
イテレートするためには途中の状態を持つ構造体TriCombiを作る必要があり、Iterator::next()を実装する必要がありますが、next()の実装難しかったです。これってジェネレータが実装されれはこの実装が不要になるんですよね？きっと。

まとめ

問題3はグラフを扱う問題だったので、ノードとエッジの構造体を作る必要があったり、あと必要ではありませんがコレクションを使ったりイテレーターを実装してみたりと、Rustでグラフやコレクションを扱う感覚が少しわかりました。
こんなプログラムを作っていると、グラフィックを扱うプログラムも作ってみたくなりますね。

関連記事

ZONeエナジー “HELLO SPACE” のrot13（Rust） ZONeエナジー “HELLO SPACE” の素数判定（Rust） Rustでオセロつくった（コマンドライン版）
開発

コメントを残す

メールアドレスが公開されることはありません。 * が付いている欄は必須項目です